
Ejercicios de programación en lenguaje C
Aquí ofrezco mi solución a otros 20 ejercicios de programación en lenguaje C pertenecientes a la asignatura de informática del Grado de Matemáticas de la Universidad de Cádiz.
Los ejercicios 1 a 20 y 21 a 40 se pueden conseguir en las siguientes entradas:
Ejercicios de lenguaje C (ejercicios 1 a 20)
Ejercicios de lenguaje C (ejercicios 21 a 40)
Si te interesa conseguir este listado de ejercicios C en formato PDF escribe a info@ejerciciosmesa.com
Listado de ejercicios de lenguaje C (ejercicios 41 a 60)
Ejercicio 41.
Realizar un programa para determinar si un año es o no bisiesto. Un año es bisiesto si es divisible por 4, pero no por 100. Como excepción a esta regla, los años divisibles por 400 sí son bisiestos. Así, 1900 no fue bisiesto, pero el año 2000 sí lo será.
Solución Ejercicio 41.
#include <stdio.h>
int main(void) {
int a;
printf("Introduzca un año: ");
scanf("%d",&a);
if( (a%4==0 && a%100!=0) || a%400==0)
printf("El año %d es bisiesto.\n",a);
else
printf("El año %d no es bisiesto.\n",a);
return 0;
}
Ejercicio 42.
El problema consiste en que dados los extremos de dos segmentos de la recta real (estos datos no se dan necesariamente en orden ascendente), determinar si los dos segmentos solapan, y si lo hacen, cual es el segmento intersección. Considerar todos los casos posibles. Por ejemplo, si los datos de entrada son 4 1 3 6, la salida será que los segmentos solapan desde el punto 3 al 4.
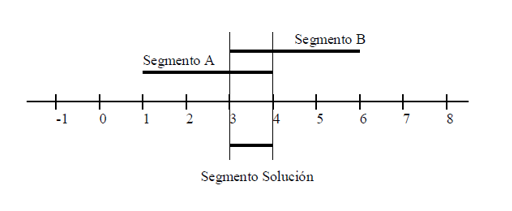
Solución Ejercicio 42.
NOTA. Para facilitar el problema, se reordenan los extremos de los segmentos A y B, usando intercambio de variables a través de una variable auxiliar.
#include <stdio.h>
int main(void) {
float a1,a2; /* segmento a */
float b1,b2; /* segmento b */
float aux;
printf("Introduzca segmento a (inicio,fin): ");
scanf("%f,%f",&a1,&a2);
printf("Introduzca segmento b (inicio,fin): ");
scanf("%f,%f",&b1,&b2);
/* reordena */
if(a1>a2) {
aux=a1;
a1=a2;
a2=aux;
}
if(b1>b2) {
aux=b1;
b1=b2;
b2=aux;
}
if(a2<b1 || b2<a1) {
printf("Los segmentos a y b no se solapan.\n");
} else if(a1<b1 && a2>b2) {
printf("Segmento solapado: %.2f, %.2f\n",b1,b2);
} else if(b1<a1 && b2>a2) {
printf("Segmento solapado: %.2f, %.2f\n",a1,a2);
} else if(a1<b1 && a2<b2) {
printf("Segmento solapado: %.2f, %.2f\n",b1,a2);
} else if(b1<a1 && b2<a2) {
printf("Segmento solapado: %.2f, %.2f\n",a1,b2);
}
return 0;
}
Ejercicio 43.
Hacer un programa para convertir de números romanos a decimal, y viceversa.
Solución Ejercicio 43.
NOTA:
Se hacen dos programas: uno para pasar de romanos a decimal y otro para pasar de decimal a romanos.
Planteamiento del problema (1) – Pasar de romano a decimal.
Se usa una cadena de caracteres para almacenar el número romano, se calcula el tamaño de la cadena (número romano) introducido y se recorre carácter a carácter.
Con cada carácter se suma un valor a una variable acumuladora llamada valor.
Si se encuentra una M se suma 1000 al valor, si se encuentra D se suma 500, etc.
Es necesario tener en cuenta aquellos valores formados por dos caracteres romanos. Por ejemplo si encontramos una C, miramos si va seguida de una D o una M, y según el caso sumanos un valor u otro:
CM – suma 900
CD – suma 400
C – suma 100
Al terminar de recorrer la cadena se muestra el valor acumulado obtenido.
#include <stdio.h>
#include <string.h>
int main(void) {
int valor=0;
int i,tam;
char romano[50];
printf("Introduzca número romano (en mayúsculas): ");
scanf("%s",romano);
tam = strlen(romano);
for(i=0;i<tam;i++) {
if(romano[i]=='I' && romano[i+1]!='V' && romano[i+1]!='X') {
valor = valor + 1;
} else if(romano[i]=='I' && romano[i+1]=='V') {
valor = valor + 4;
i++; /* esto es para saltarse la V, ya que ha sido contada */
} else if(romano[i]=='V') {
valor = valor + 5;
} else if(romano[i]=='I' && romano[i+1]=='X') {
valor = valor + 9;
i++; /* esto es para saltarse la X, ya que ha sido contada */
} else if(romano[i]=='X' && romano[i+1]!='L' && romano[i+1]!='C') {
valor = valor + 10;
} else if(romano[i]=='X' && romano[i+1]=='L') {
valor = valor + 40;
i++; /* esto es para saltarse la L, ya que ha sido contada */
} else if(romano[i]=='L') {
valor = valor + 50;
} else if(romano[i]=='X' && romano[i+1]=='C') {
valor = valor + 90;
i++; /* esto es para saltarse la C, ya que ha sido contada */
} else if(romano[i]=='C' && romano[i+1]!='D' && romano[i+1]!='M') {
valor = valor + 100;
} else if(romano[i]=='C' && romano[i+1]=='D') {
valor = valor + 400;
i++; /* esto es para saltarse la D, ya que ha sido contada */
} else if(romano[i]=='D') {
valor = valor + 500;
} else if(romano[i]=='C' && romano[i+1]=='M') {
valor = valor + 900;
i++; /* esto es para saltarse la M, ya que ha sido contada */
} else if(romano[i]=='M') {
valor = valor + 1000;
}
}
printf("El número romano es el %d\n",valor);
return 0;
}
Planteamiento del problema (2) – Pasar de decimal a romano.
Para pasar de decimal a romanos consideramos un rango (0, 3400) representable.
El proceso es el siguiente:
Si el número es mayor o igual a 1000, se calcula el cociente entre el número y 1000 para saber cuantas ‘M’ hay que introducir en la cadena del número romano.
A continuación se calcula el resto del número a representar.
Si el número es mayor o igual a 900, se introduce una ‘CM’ en la cadena del número romano, y se calcula el resto del número a representar.
Si el número es mayor o igual a 500, se introduce una ‘D’ e la cadena del número romano, y se calcula el resto del número a representar.
Esta idea se repite con los siguientes valores representativos de un número romano, que son:
400 – CD
100/200/300 – C / CC / CCC
90 – XC
50 – L
40 – XL
10/20/30 – X / XX / XXX
9 – IX
5 – V
4 – IV
1/2/3 – I / II / III
Al finalizar el programa es importante cerrar la cadena de caracteres del número romano con el valor de fin de cadena ‘\0’ para que no se produzca error al imprimirla en pantalla.
#include <stdio.h>
#include <string.h>
int main(void) {
int n;
int i,j,d; /* contadores */
char romano[50]; /* cadena para representar el número romano */
printf("Introduzca un número mayor de 0 y menor de 3400: ");
scanf("%d",&n);
if(n>=0 && n<3400) {
i=0; /* indice para almacenar cada caracter romano */
while(n>=1) {
if(n>=1000) {
d = n/1000;
for(j=0;j<d;j++) {
/* introduce una M y aumenta el índice */
romano[i++]='M';
}
/* obtiene el resto del número a representar */
n = n % (d*1000);
} else if(n>=900) {
romano[i++]='C';
romano[i++]='M';
n = n % 900;
} else if(n>=500) {
romano[i++]='D';
n = n % 500;
} else if(n>=400) {
romano[i++]='C';
romano[i++]='D';
n = n % 400;
} else if(n>=100) {
d = n/100;
for(j=0;j<d;j++) {
romano[i++]='C';
}
n = n % (d*100);
} else if(n>=90) {
romano[i++]='X';
romano[i++]='C';
n = n % 90;
} else if(n>=50) {
romano[i++]='L';
n = n % 50;
} else if(n>=40) {
romano[i++]='X';
romano[i++]='L';
n = n % 40;
} else if(n>=10) {
d = n/10;
for(j=0;j<d;j++) {
romano[i++]='X';
}
n = n % (d*10);
} else if(n>=9) {
romano[i++]='I';
romano[i++]='X';
n = n % 9;
} else if(n>=5) {
romano[i++]='V';
n = n % 5;
} else if(n>=4) {
romano[i++]='I';
romano[i++]='V';
n = n % 4;
} else if(n>=1) {
for(j=0;j<n;j++) {
romano[i++]='I';
}
n=0;
}
}
romano[i]='\0'; /* es necesario finalizar la cadena con \0 */
printf("El numero en romano es: %s\n",romano);
} else {
printf("El número introducio no es válido.\n");
}
return 0;
}
Ejercicio 44.
Hacer un programa que descomponga un número en sus factores primos.
Solución Ejercicio 44.
#include <stdio.h>
int main(void) {
int n,i,exp;
printf("Introduzca numero: ");
scanf("%d",&n);
printf("Descomposición en factores primos: ");
i=2; /* primer factor a comprobar */
while(n>1) {
if(n%i==0) { /* si encuentro un divisor... */
exp=0;
/* divido sucesivamente para saber su potencia */
while(n%i==0) {
n=n/i;
exp++;
}
printf("%d^%d ",i,exp); /* imprimo el factor encontrado */
}
i++; /* paso al siguiente número a comprobar */
}
return 0;
}
Ejercicio 45.
Un borracho realiza una marcha aleatoria siguiendo las siguientes reglas. El borracho parte del punto (0,0). En los tiempos t=1,2,3,4,… el borracho da un paso en uno de los cuatro sentidos (arriba, abajo, derecha o izquierda). La caminata termina cuando el borracho se sale del círculo de radio R y centro (0,0). Determine experimentalmente la longitud de la caminata del borracho para R=10.
Como la longitud de la caminata no siempre es la misma, repetir el experimento 100 veces, y dar como resultado el valor medio.
Solución Ejercicio 45.
Planteamiento del problema
El programa genera números aleatorios entre 0 y 3 usando la función rand(), y la función srand() como semilla para la generación aleatoria. Para facilitar la comprensión del código se crean 4 constantes (usando enum) llamadas ARRIBA, ABAJO, DERECHA e IZQUIERDA correspondientes a los valores 0, 1, 2 y 3 generados aleatoriamente.
El programa genera aleatoriamente una dirección, actualiza la posición (x,y) del borracho, le suma 1 a un acumulador de longitud, y calcula la distancia de la nueva posición al centro. Esto se repite hasta que la distancia al centro sea mayor que 10.
El código anterior se repite 100 veces, sumando las longitudes obtenidas en un acumulador suma, que luego servirá para calcular la media.
Todo el proceso es monitorizado imprimiendo las direcciones generadas de cada caminata y los valores de la longitud obtenidos.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define R 10 /* radio 10 */
#define CAMINATAS 100 /* número de caminatas */
enum {ARRIBA, ABAJO, DERECHA, IZQUIERDA};
/* ARRIBA = 0, ABAJO = 1, DERECHA = 2, IZQUIERDA = 3 */
int main(void) {
int x,y; /* posición del borracho */
int longitud,i,suma;
int dir; /* direccion arriba, abajo, derecha, izquierda */
float dis; /* distancia al centro */
float media;
srand(time(NULL)); /* semilla para números aleatorios */
suma=0;
for(i=0;i<CAMINATAS;i++) {
printf("Caminata %d:\n\n",i+1);
longitud=0;x=0;y=0;
do {
dir = rand()%4; /* numero aleatorio entre 0 y 3 */
if(dir==ARRIBA) y++;
else if(dir==ABAJO) y--;
else if(dir==DERECHA) x++;
else if(dir==IZQUIERDA) x--;
switch(dir) {
case ARRIBA:
printf("ARRIBA ");break;
case ABAJO:
printf("ABAJO ");break;
case DERECHA:
printf("DERECHA ");break;
case IZQUIERDA:
printf("IZQUIERDA ");break;
}
longitud++;
dis = sqrt(pow(x,2)+pow(y,2));
} while(dis<=R);
printf("\n\nDistancia al centro: %.2f. Longitud recorrida:
%d\n\n",dis,longitud);
suma += longitud;
}
media = suma / CAMINATAS;
printf("\n\nLa media de las distancias recorridas es %.2f\n",media);
return 0;
}
Ejercicio 46.
Otra versión del problema del borracho dice que ahora el borracho se encuentra en un extremo de un puente cuya anchura son, por ejemplo, 5 pasos. El borracho parte del centro del puente, y da un paso adelante. La probabilidad de que dé un paso torcido hacia la izquierda, hacia la derecha o sin torcer son idénticas e iguales a 1/3. Determinar experimentalmente cuál es la relación entre la anchura del puente y la longitud del mismo, para que haya más posibilidades de que el borracho cruce el puente a que se caiga en su paseo aleatorio. Veamos un ejemplo de paseo:
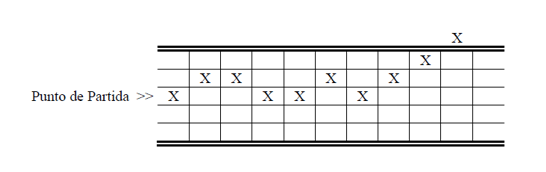
Solución Ejercicio 46.
Planteamiento del problema
Se establece una longitud para el puente fija de 100, y un alto inicial de 5.
Aleatoriamente, se genera un número entre 0 y 2 (ARRIBA – 0, ABAJO – 1, CENTRO – 2), y según el número que sale se cambia la posición (y) del borracho. La posición x aumenta en 1.
Este proceso se repite hasta que la posición vertical supera el alto del puente o pasa a ser menor que 0. O bien, la posición x llega al final del puente.
Si el borracho alcanza el final del puente se aumenta un contador completados a 1. Se repite el experimento 100 veces, por lo que completados equivale al porcentaje de aciertos.
Todo lo anterior se repite aumentando el alto del puente (de dos en dos para garantizar una celda de partida centrada) y dejando el ancho fijo. Para cada configuración del puente se calcula el porcentaje de aciertos (completados) y el proceso finaliza cuando el porcentaje conseguido es mayor de un 90%.
Se muestra entonces en pantalla el ancho y alto del puente final y su relación. También se monitoriza todo el programa mostrando los resultados de los distintos puentes configurados.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define PORCENTAJEMIN 90
enum {ARRIBA,ABAJO};
/* ARRIBA = 0, ABAJO = 1 */
int main(void) {
int x,y,i;
int ancho,alto;
int avance,completados;
srand(time(NULL)); /* semilla para números aleatorios */
alto=5;
ancho=100;
do {
completados=0;
for(i=0;i<100;i++) {
x=0;
y=(alto)/2;
do {
avance = rand()%3;
x++;
if(avance==ARRIBA) y++;
else if(avance==ABAJO) y--;
} while(y<alto && y>=0 && x<ancho);
if(x==ancho) completados++;
}
printf("Ancho %d, Alto %d. Porcentaje completados:
%d.\n",ancho,alto,completados);
alto+=2;
} while(completados<PORCENTAJEMIN);
printf("\nPorcentaje de aciertos: %d. Ancho: %d, Alto %d, Relación
ancho/alto: %.2f\n",
completados,ancho,alto,(float)ancho/(float)alto);
return 0;
}
Ejercicio 47.
Se puede determinar el valor de PI, sabiendo que el área de un círculo es PI · r2 . Realizar un programa que obtenga una buena aproximación de PI, utilizando el método de MonteCarlo. Para ello, generar N puntos (xi, yi, i=1,2,…N), y utilizar en el cálculo cuántos caen dentro del círculo de centro (0,0) y radio 1.
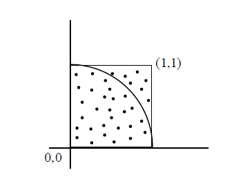
Solución Ejercicio 47.
Planteamiento del problema
Método de Montecarlo. Sea un cuadrado de lado 2 en el que está inscrito un círculo de radio 1. Si se tienen n puntos distribuidos de forma uniforme dentro del cuadrado, se debe cumplir lo siguiente:
La totalidad de puntos (n) se corresponde (cubren) la superficie de todo el cuadrado (4)
Los x puntos que estén a una distancia del centro del círculo menor o igual a 1 (puntos que están dentro del círculo), se corresponden con el área del círculo, que es p · r2 , es decir, p , ya que el radio es 1.
Por tanto: n => 4, x => pi. Así pues: pi = 4 * x / n
Pi se puede entonces calcular multiplicando 4 por el número de puntos en el interior del círculo dividido por la totalidad de puntos.
Para generar números aleatorios, se usa la función sram para generar una semilla de números aleatorios. Luego se usa la función rand() que genera números aleatorios entre 0 y el valor máximo RAND_MAX. Al calcular el resto de rand() entre 1001 se obtienen números aleatorios entre 0 y 1000. El resultado se divide entre 1000 para obtener valores entre 0 y 1, correspondientes a las coordenadas aleatorias de los puntos distribuidos en la superficie del cuadrado.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
int main(void) {
float x,y,d,pi;
unsigned n,i,ndentro=0;
srand(time(NULL));
printf("Introduzca número de puntos: ");
scanf("%d",&n);
for(i=0;i<n;i++) {
x = (rand()%1001) / 1000.0;
y = (rand()%1001) / 1000.0;
d = sqrt(pow(x,2)+pow(y,2));
if(d<=1) ndentro++;
}
pi = ndentro*4.0/(float)n;
printf("La aproximación de PI es: %f\n",pi);
return 0;
}
Ejercicio 48.
Se puede determinar una aproximación del área de la curva y = 2 · x 2 entre los puntos x=0 y x=1 tomando de forma aleatoria un cierto número de puntos en el cuadrado formado por el punto(0,0) y el punto(1,1). El área se puede determinar a partir de la relación entre el número de puntos bajo la curva y el número total de puntos. Por supuesto, si el número de puntos seleccionados es muy grande, la aproximación es más fiable. La aproximación en el ejemplo es 12/19, muy cercana al valor real 2/3. Esta técnica matemática para aproximar valores se denomina método de MonteCarlo. Realizar el correspondiente programa para calcular áreas de funciones polinómicas sencillas entre dos puntos dados.
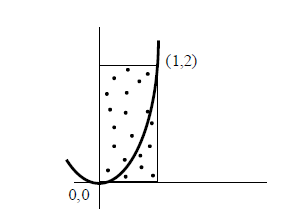
Solución Ejercicio 48.
Planteamiento del problema
Se considerarán polinomios de segundo grado: a x2 + b x + c. Por tanto, el usuario tendrá que introducir los valores a, b y c, y los valores para el intervalo de x: x1 y x2. También introducirá el número de puntos (n) que quiere generar en la superficie comprendida entre (x1,y1) y (x2,y2)
El programa empieza calculando los valores de la función para x1 y x2, que son y1 e y2.
A continuación inicializa una variable contadora debajo, que contará los puntos bajo la curva.
Y genera un total de n puntos aleatorios dentro de la superficie (x1,y1) (x2,y2). Calcula inicialmente un valor aleatorio xa comprendido entre x1 y x2, y para xa calcula el valor de la función f. A continuación calcula un valor aleatorio ya comprendido entre y1 e y2, y comprueba si ya es menor que f. En ese caso aumenta el contador debajo.
Para calcular el área hay que tener en cuenta lo siguiente:
Si n puntos se corresponde con el área total: |x2-x1| * |y2-y1|
Entonces debajo puntos se corresponde con area.
area = debajo * |x2-x1| * |y2-y1| / n
Para generar las x aleatorias, se hace lo siguiente:
Se multiplica la distancia entre x1 y x2 por 1000, y se genera un número aleatorio dentro de dicho rango, para luego dividirlo entre 1000 para volver a obtener un valor menor que la distancia entre x1 y x2. Finalmente se le suma x1 al valor obtenido para que el resultado esté dentro del rango [x1,x2].
Esta misma idea se aplica para calcular y aleatorias.
Ejemplo: x1=3, x2=5
Distancia: 2 por 1000 = 2000
Se genera un valor aleatorio entre 0 y 2000, digamos, el 1534.
Se divide entre 1000: 1,534
Este valor se suma a 3, por lo que se obtiene 4,534 (un valor aleatorio que está entre 3 y 5)
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <time.h>
int main(void) {
int x1,x2,y1,y2,n,i;
int a,b,c; /* fx = ax^2 + bx + c */
float xa,ya,f; /* punto aleatorio, valor de la función */
int debajo; /* número de puntos debajo de la curva */
float area;
srand(time(NULL)); /* semilla para números aleatorios */
printf("Introduzca a,b,c para el polinomio: ");
scanf("%d,%d,%d",&a,&b,&c);
printf("Introduzca x1,x2: ");
scanf("%d,%d",&x1,&x2);
printf("Introduzca el número de puntos a generar: ");
scanf("%d",&n);
y1 = a*pow(x1,2)+b*x1+c;
y2 = a*pow(x2,2)+b*x2+c;
debajo=0;
for(i=0;i<n;i++) {
xa = x1 + ((float)(rand()%(abs(x2-x1)*1000)+1))/1000.0;
f = a*pow(xa,2)+b*xa+c;
ya = y1 + ((float)(rand()%(abs(y2-y1)*1000)+1))/1000.0;
if(ya<f) debajo++;
}
area = (abs(x2-x1)*abs(y2-y1) * debajo) / (float) n;
printf("El area bajo la curva es %.4f\n",area);
return 0;
}
Ejercicio 49.
Haz un programa que permita traducir entre grados Celsius (C), Fahrenheit (F), Kelvin (K) y Rankine (R). El programa preguntará en qué unidades damos la temperatura de entrada y a qué escala la queremos convertir.
Solución Ejercicio 49.
Planteamiento del problema
En algunas conversiones uso la fórmula directamente, mientras que en otras primero paso a Centígrados y luego convierto de Centígrados a la unidad correspondiente.
#include <stdio.h>
int main(void) {
int unidad_e, unidad_s; /* unidad de entrada y salida */
float temp_e, temp_s; /* temperatura de entrada y salida */
float temp_aux; /* temperatura auxiliar */
printf("Introduzca unidad de entrada (1 - C, 2 - F, 3 - K, 4 - R): ");
scanf("%d",&unidad_e);
printf("Introduzca temperatura: ");
scanf("%f",&temp_e);
printf("Introduzca unidad de salida (1 - C, 2 - F, 3 - K, 4 - R): ");
scanf("%d",&unidad_s);
if(unidad_e < 1 || unidad_e > 4) {
printf("Error en la unidad de entrada elegida.\n");
} else if(unidad_s < 1 || unidad_s > 4) {
printf("Error en la unidad de salida elegida.\n");
} else if(unidad_e == unidad_s) {
printf("La unidad de salida debe ser distinta a la de entrada.\n");
} else {
if(unidad_e==1) { /* Centígrados */
if(unidad_s==2) { /* C -> F */
temp_s = (temp_e * (9.0/5.0)) + 32; /* F = (9*C/5) + 32 */
printf("%.2f C = %.2f F\n",temp_e,temp_s);
} else if(unidad_s==3) { /* C -> K */
temp_s = temp_e + 273.15; /* K = C + 273.15 */
printf("%.2f C = %.2f K\n",temp_e,temp_s);
} else if(unidad_s==4) { /* C -> R */
/* R = F + 459.67 y sustituyendo F... */
temp_s = (temp_e * (9.0/5.0)) + 32 + 459.67;
printf("%.2f C = %.2f R\n",temp_e,temp_s);
}
} else if(unidad_e==2) { /* Fahrenheit */
if(unidad_s==1) { /* F -> C */
temp_s = (temp_e - 32) * (5.0/9.0); /* C = (5/9)*(F-32) */
printf("%.2f F = %.2f C\n",temp_e,temp_s);
} else if(unidad_s==3) { /* F -> K */
temp_aux = (temp_e - 32) * (5.0/9.0); /* paso F -> C */
temp_s = temp_aux + 273.15; /* y C -> K */
printf("%.2f F = %.2f K\n",temp_e,temp_s);
} else if(unidad_s==4) { /* F -> R */
temp_aux = (temp_e - 32) * (5.0/9.0); /* paso F -> C */
temp_s = (temp_aux * (9.0/5.0)) + 32 + 459.67; /* y C -> R */
printf("%.2f F = %.2f R\n",temp_e,temp_s);
}
} else if(unidad_e==3) { /* Kelvin */
if(unidad_s==1) { /* K -> C */
temp_s = temp_e - 273.15; /* C = K - 273.15 */
printf("%.2f K = %.2f C\n",temp_e,temp_s);
} else if(unidad_s==2) { /* K -> F */
temp_aux = temp_e - 273.15; /* paso K a C */
temp_s = (temp_aux * (9.0/5.0)) + 32; /* y C a F */
printf("%.2f K = %.2f F\n",temp_e,temp_s);
} else if(unidad_s==4) { /* K -> R */
temp_aux = temp_e - 273.15; /* paso K a C */
temp_s = (temp_aux * (9.0/5.0)) + 32 + 459.67; /* y C -> R */
printf("%.2f K = %.2f R\n",temp_e,temp_s);
}
} else if(unidad_e==4) { /* Rankine */
if(unidad_s==1) { /* R -> C */
/* C = (R - 491.67) * (5/9) */
temp_s = (temp_e - 491.67) * (5.0/9.0);
printf("%.2f R = %.2f C\n",temp_e,temp_s);
} else if(unidad_s==2) { /* R -> F */
temp_aux = (temp_e - 491.67) * (5.0/9.0); /* paso R a C */
temp_s = (temp_aux * (9.0/5.0)) + 32; /* y C a F */
printf("%.2f R = %.2f F\n",temp_e,temp_s);
} else if(unidad_s==3) { /* R -> K */
temp_aux = (temp_e - 491.67) * (5.0/9.0); /* paso R a C */
temp_s = temp_aux + 273.15; /* K = C + 273.15 */
printf("%.2f R = %.2f K\n",temp_e,temp_s);
}
}
}
return 0;
}
Ejercicio 50.
Haz un programa que lea los datos que definen un círculo (centro y radio) y las coordenadas de un punto en el espacio. El programa deberá decirnos si el punto está o no dentro del círculo.
Solución Ejercicio 50.
#include <stdio.h>
#include <math.h>
int main(void) {
float xc,yc,rc; /* coordenadas centro circulo y radio */
float xp,yp; /* coordenadas del punto */
float d; /* distancia */
printf("Introduce las coordenadas del centro del circulo (x,y): ");
scanf("%f,%f",&xc,&yc);
printf("Introduce el radio del circulo: ");
scanf("%f",&rc);
printf("Introduce las coordenadas del punto (x,y): ");
scanf("%f,%f",&xp,&yp);
/* se calcula la distancia entre el centro del circulo y el punto */
d = sqrt(pow(xp-xc,2)+pow(yp-yc,2));
if(d<=rc) { /* si esa distancia es menor que el radio */
printf("El punto esta dentro del circulo\n");
} else {
printf("El punto esta fuera del circulo\n");
}
return 0;
}
Ejercicio 51.
Haz un programa que lea las coordenadas que definen un rectángulo (esquina superior y esquina inferior opuesta) y las coordenadas de un punto en el espacio. El programa deberá decirnos si el punto está o no dentro del rectángulo.
Solución Ejercicio 51.
Planteamiento del problema
Fuerzo al usuario a introducir primero la esquina superior izquierda y luego la esquina inferior derecha para facilitar los cálculos.
#include <stdio.h>
#include <math.h>
int main(void) {
float xr1,yr1,xr2,yr2; /* coordenadas rectangulo */
float xp,yp; /* coordenadas del punto */
printf("Introduce las coordenadas de la esquina superior izquierda: ");
scanf("%f,%f",&xr1,&yr1);
printf("Introduce las coordenadas de la esquina inferior derecha: ");
scanf("%f,%f",&xr2,&yr2);
printf("Introduce las coordenadas del punto (x,y): ");
scanf("%f,%f",&xp,&yp);
if(xr1 < xr2 && yr1 > yr2) { /* datos correctos */
if(xp>=xr1 && xp<=xr2 && yp<=yr1 && yp>=yr2) {
printf("El punto esta dentro del rectangulo\n");
} else {
printf("El punto no esta dentro del rectangulo\n");
}
} else {
printf("Debe introducir correctamente las coordenadas de las
esquinas\n");
}
return 0;
}
Ejercicio 52.
Hacer un programa que lea las coordenadas de tres puntos y diga si forman o no un triángulo. Determinar qué tipo de triángulo es de acuerdo a los siguientes casos. Suponiendo que A corresponde al mayor de los tres lados y B y C a los otros dos, entonces:
- Si A >= B + C entonces: No es un triángulo
- Si A^2 = B^2 + C^2 entonces: Es un triángulo rectángulo
- Si A^2 > B^2 + C^2 entonces: Es un triángulo obtusángulo
- Si A^2 < B^2 + C^2 entonces: Es un triángulo acutángulo
Solución Ejercicio 52.
#include <stdio.h>
#include <math.h>
int main(void) {
float x1,y1,x2,y2,x3,y3; /* coordenadas puntos triangulo */
float a,b,c; /* longitud lados */
float A,B,C; /* lados, donde A es el mayor */
printf("Introduce las coordenadas del punto 1: ");
scanf("%f,%f",&x1,&y1);
printf("Introduce las coordenadas del punto 2: ");
scanf("%f,%f",&x2,&y2);
printf("Introduce las coordenadas del punto 3: ");
scanf("%f,%f",&x3,&y3);
/* a = distancia punto 1 y 2 */
a = sqrt(pow(x1-x2,2)+pow(y1-y2,2));
/* b = distancia punto 1 y 3 */
b = sqrt(pow(x1-x3,2)+pow(y1-y3,2));
/* c = distancia punto 2 y 3 */
c = sqrt(pow(x2-x3,2)+pow(y2-y3,2));
/* reordeno los lados, haciendo A el mayor */
if(a>=b && a>=c) {
A = a;
B = b;
C = c;
} else if(b>=a && b>=c) {
A = b;
B = a;
C = c;
} else if(c>=a && c>=b) {
A = c;
B = b;
C = a;
}
if(A>=(B+C)) {
printf("No es un triangulo\n");
} else if((A*A) == (B*B+C*C)) {
printf("Es un triangulo rectangulo\n");
} else if((A*A) > (B*B+C*C)) {
printf("Es un triangulo obtusangulo\n");
} else if((A*A) < (B*B+C*C)) {
printf("Es un triangulo acutangulo\n");
}
return 0;
}
Ejercicio 53.
La distancia del punto de caída de un proyectil que es lanzado con un ángulo Angulo (expresado en radianes) con una velocidad inicial de Velocidad (expresado en pies por segundo), ignorando la resistencia del aire, viene dada por la fórmula:
Distancia=Velocidad^2∗ seno(2∗ Angulo)/32.2
Escribir un programa que realice un juego en el que el usuario introduce primero la distancia a una diana. Luego el usuario introduce el ángulo y la velocidad de lanzamiento de un proyectil. Si el proyectil cae dentro de un diez por ciento de la distancia a la diana, el usuario gana el juego. Si el proyectil no se acerca lo suficiente, se le dice al usuario cuanto se ha alejado el proyectil. Para simplificar las entradas del usuario, el programa debe permitir que el ángulo de la entrada se de en grados.
Solución Ejercicio 53.
#include <stdio.h>
#include <math.h>
int main(void) {
float ar,ag; /* angulo en radianes y grados */
float v,d; /* velocidad y distancia */
float dd; /* distancia del disparo */
float fin = 0; /* bandera fin juego */
float PI = acos(-1); /* PI es igual al arcocoseno de -1 */
printf("Introduce la distancia a la diana: ");
scanf("%f",&d);
do {
printf("Introduce velocidad: ");
scanf("%f",&v);
printf("Introduce angulo en grados: ");
scanf("%f",&ag);
ar = ag * PI/180.0;
dd = v*v*sin(2*ar)/32.2;
printf("Distancia del disparo: %.2f\n",dd);
if(dd>d) {
printf("Te has pasado\n");
} else if(dd==d) {
printf("Acertaste de pleno!!!\n");
fin = 1;
} else if(dd<d) {
if(dd>=(d-d*0.1)) { /* esta dentro del 10% */
printf("Esta dentro del 10%%!!!"); /* %% imprime el % */
fin = 1;
} else {
printf("Te has quedado corto\n");
}
}
} while(!fin); /* repetir mientras no aciertes */
return 0;
}
Ejercicio 54.
Diseña un programa al que se de cómo entrada dos enteros y un carácter. El programa deberá sumar, restar, multiplicar o dividir los valores de los dos enteros dependiendo del código indicado en el tercer parámetro, y devolver el resultado.
Solución Ejercicio 54.
Planteamiento del problema
Resuelvo el problema considerando que los valores son introducidos desde teclado, y no como parámetros de la función main.
#include <stdio.h>
int main(void) {
int a,b; /* dos enteros */
char c; /* caracter */
printf("Introduce entero a: ");
scanf("%d",&a);
printf("Introduce entero b: ");
scanf("%d",&b);
printf("Introduce caracter (+,-,*,/): ");
fflush(stdin);
scanf("%c",&c);
switch(c) {
case '+':
printf("%d + %d = %d\n",a,b,a+b);
break;
case '-':
printf("%d - %d = %d\n",a,b,a-b);
break;
case '*':
printf("%d * %d = %d\n",a,b,a*b);
break;
case '/':
printf("%d / %d = %d\n",a,b,a/b);
break;
default:
printf("Operacion no valida\n");
}
return 0;
}
Ejercicio 55.
Escriba una función que reciba como parámetros los coeficientes a, b, c y d y la variable x, y calcule p, el valor del correspondiente polinomio de grado 3:
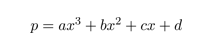
Solución Ejercicio 55.
#include <stdio.h>
float polinomio3(float x, float a, float b, float c, float d) {
return a*x*x*x+b*x*x+c*x+d;
}
int main(void) {
float x, a, b, c, d, p;
printf("Introduce x, a, b, c, d: ");
scanf("%f,%f,%f,%f,%f",&x,&a,&b,&c,&d);
p = polinomio3(x,a,b,c,d);
printf("El valor del polinomio es %.2f\n",p);
return 0;
}
Ejercicio 56.
Escriba una función que reciba las coordenadas de dos puntos, y calcule su distancia euclídea.
Solución Ejercicio 56.
#include <stdio.h>
#include <math.h>
float distancia(float x1, float y1, float x2, float y2) {
return sqrt(pow(x1-x2,2)+pow(y1-y2,2));
}
int main(void) {
float x1,y1,x2,y2,d;
printf("Introduce punto 1 (x,y): ");
scanf("%f,%f",&x1,&y1);
printf("Introduce punto 2 (x,y): ");
scanf("%f,%f",&x2,&y2);
d = distancia(x1,y1,x2,y2);
printf("La distancia entre los dos puntos es %.2f\n",d);
return 0;
}
Ejercicio 57.
Escriba una función que calcule el factorial de un número.
Solución Ejercicio 57.
#include <stdio.h>
float factorial(int n) {
float f = 1;
int i;
for(i=n;i>1;i--) f = f * i;
return f;
}
int main(void) {
int n;
float f;
printf("Introduce un numero: ");
scanf("%d",&n);
f = factorial(n);
printf("El factorial de %d es %.0f\n",n,f);
return 0;
}
Ejercicio 58.
Escriba una función que permita convertir una temperatura de grados Farenheit a grados Celsius, y viceversa.
Solución Ejercicio 58.
#include <stdio.h>
/*
* Si conversión es 0, temp se considera Celsius y se convierte a Fahrenheit
* Si conversión es otro número, temp se considera Fahrenheit y se convierte a Celsius
*/
float CelFa(float temp, int conversion) {
if(conversion==0) { /* C -> F */
return (temp * (9.0/5.0) + 32);
} else { /* F -> C */
return (temp - 32) * (5.0/9.0);
}
}
int main(void) {
float temp,tempconv; /* temperatura entrada, temperatura convertida */
int conv;
printf("Tipo de conversion (0 C->F, 1 F->C): ");
scanf("%d",&conv);
printf("Introduzca temperatura: ");
scanf("%f",&temp);
if(conv==0) {
tempconv = CelFa(temp,conv);
printf("%f Celsius = %f Fahrenheit\n",temp,tempconv);
} else {
tempconv = CelFa(temp,conv);
printf("%f Fahrenheit = %f Celsius\n",temp,tempconv);
}
return 0;
}
Ejercicio 59.
Escribir una función que calcule si un número es primo.
Solución Ejercicio 59.
#include <stdio.h>
/*
* Devuelve 1 (verdadero) si el número n es primo
* Devuelve 0 (falso) si el número n no es primo
*/
int primo(int n) {
int i;
/* se comprueban posibles divisores distintos de 1 y n */
for(i=2;i<n/2;i++) { /* no es necesario comprobar a partir de n/2 */
if(n%i==0) { /* i es divisor */
return 0; /* no es primo */
}
}
/* si llegó aquí, es que no encontró divisor, por lo que es primo */
return 1;
}
int main(void) {
int n;
printf("Introduzca un numero: ");
scanf("%d",&n);
if(primo(n)) { /* equivalente a if(primo(n)==1) */
printf("El numero %d es primo\n",n);
} else {
printf("El numero %d no es primo\n",n);
}
return 0;
}
Ejercicio 60.
Descomponer un número entero en sus factores primos.
Solución Ejercicio 60.
#include <stdio.h>
void factoresprimos(int n) {
int f=2; /* primer posible factor primo */
int exp; /* exponente */
printf("%d = ",n);
while(n>1) {
if(n%f==0) { /*encontre un divisor */
exp = 0; /* exponente a 0 */
while(n%f==0) {
/* voy dividiendo n sucesivamente mientras sea divisible por f */
n = n/f;
exp++; /* y sumo 1 al exponente */
}
/* muestro el factor primo con su exponente */
printf("%d^%d ",f,exp);
}
f++; /* siguiente posible divisor a comprobar */
}
}
int main(void) {
int n;
printf("Introduzca un numero: ");
scanf("%d",&n);
factoresprimos(n);
return 0;
}
Puedes acceder a más recursos formativos, ejercicios resueltos de programación, test de informática, etc., en ejerciciosmesa.com. También tienes disponibles juegos de lógica e interactivos en mesagames.es.
