
Ejercicios de programación en lenguaje C
A continuación ofrezco la solución a 20 ejercicios más sobre resolución de problemas usando programación en lenguaje C. Estos ejercicios pertenecen a la asignatura de informática del Grado de Matemáticas de la Universidad de Cádiz.
Los primeros 20 ejercicios del listado ya resueltos pueden conseguirse en la siguiente entrada:
Ejercicios de lenguaje C (ejercicios 1 a 20)
Si te interesa conseguir este listado de ejercicios C en formato PDF puedes escribir a info@ejerciciosmesa.com
Listado de ejercicios de lenguaje C (ejercicios 21 a 40)
Ejercicio 21.
Escribir un programa que lea 3 números que representan una hora con el formato hh:mm:ss, y diga si es una hora correcta o no.
Solución Ejercicio 21.
#include <stdio.h>
int main(void) {
int hh,mm,ss; /* horas, minutos, segundos */
printf("Introduzca hora (hh:mm:ss): ");
scanf("%d:%d:%d",&hh,&mm,&ss);
if(hh>=0 && hh<24 && mm>=0 && mm<60 && ss>=0 && ss<60) {
printf("La hora introducida es correcta.\n");
} else {
printf("La hora introducida no es correcta.\n");
}
return 0;
}
Ejercicio 22.
Escribir un programa que lea un número (a) y una base (b), y calcule el logaritmo en base b de a. Por ejemplo, si a=36, y b=6, el programa debe imprimir 2, ya que 6 elevado a 2 es 36.
Solución Ejercicio 22.
Planteamiento del problema
Una forma sencilla de realizar el programa es usando la función log, de la librería math.h. Esta función calcula el logaritmo natural de un número. Sin embargo, puesto que se cumple que:
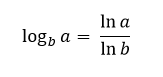
calculando log(a) y log(b) y dividiéndolos, obtendremos logb a. Se tiene en cuenta que el número a debe ser un real mayor que 0, y que la base debe ser entera positiva mayor o igual a 1.
#include <stdio.h>
#include <math.h>
int main(void) {
float a,lo; /* queremos calcular lo = logaritmo en base b de a */
int b;
printf("Introduzca número: ");
scanf("%f",&a);
printf("Introduzca base: ");
scanf("%d",&b);
if(b<1) {
printf("Error. La base debe ser mayor o igual a 1.\n");
} else if(a<=0) {
printf("Error. El número debe ser mayor que 0.\n");
} else {
lo = log(a) / log(b);
printf("Logaritmo en base %d de %.2f es %.2f\n",b,a,lo);
}
return 0;
}
Ejercicio 23.
Escribir un programa que lea un número de segundos (N), y escriba por pantalla un mensaje similar a éste. Sea N = 7540.
7540 segundos es lo mismo que 2 horas, 5 minutos y 40 segundos
Solución Ejercicio 23.
Planteamiento del problema
En una hora hay 3600 segundos. Por tanto, para saber cuantas horas hay en 7540 segundos hacemos la división: 7540/3600. El resultado son 2 horas.
Si calculamos el resto de la división 7540/3600, obtendremos los segundos restantes. Esto es: 340 segundos.
Ahora dividimos 340/60 para saber cuantos minutos son. Son 5 minutos. Y si calculamos el resto de 340/60, obtenemos los segundos restantes, que son 40.
#include <stdio.h>
int main(void) {
int nseg; /* número de segundos introducidos */
int saux; /* variable auxiliar */
int s,m,h; /* segundos, minutos y horas */
printf("Introduzca segundos: ");
scanf("%d",&nseg);
/* En una hora hay 3600 segundos. */
h = nseg / 3600;
saux = nseg % 3600; /* el resto proporciona los segundos restantes */
m = saux / 60; /* en un minuto hay 60 segundos */
s = saux % 60; /* el resto proporciona los segundos que quedan */
printf("%d segundos es lo mismo que %d horas, %d minutos y %d
segundos.\n",nseg,h,m,s);
return 0;
}
Ejercicio 24.
Escriba un programa que escriba los números del 1 al 100, saltando de línea cada 10 números.
Solución Ejercicio 24.
#include <stdio.h>
int main(void) {
int i;
for(i=1;i<=100;i++) {
printf("%d ",i);
/* si el número i es divisible por 10, salto de línea */
if(i%10==0) {
printf("\n");
}
}
return 0;
}
Ejercicio 25.
Escriba un programa que sume los números impares del 1 al 100.
Solución Ejercicio 25.
#include <stdio.h>
int main(void) {
int i;
int suma = 0; /* se inicializa la suma a 0 */
for(i=1;i<=100;i+=2) { /* i+=2 hace que avance de dos en dos */
suma += i; /* es equivalente a suma = suma + i; */
}
printf("La suma de los números impares es: %d\n",suma);
return 0;
}
Ejercicio 26.
Escriba un programa que escriba los múltiplos de un nº leído desde teclado comprendidos entre el 1 y el 100.
Solución Ejercicio 26.
#include <stdio.h>
int main(void) {
int i,n,multiplo;
printf("Introduzca un número entre 1 y 100: ");
scanf("%d",&n);
if(n<1 || n>100) {
printf("Error, el número no es válido.\n");
} else {
printf("Los múltiplos del número comprendidos entre 1 y 100 son: ");
i=1;
multiplo=n;
while(multiplo<=100) { /* solo entre 1 y 100 */
printf("%d ",multiplo); /* imprimo el múltiplo */
i++; /* incremento i en 1 */
multiplo = n * i; /* calculo el nuevo múltiplo */
}
}
return 0;
}
Ejercicio 27.
Escribir un programa que calcule cuánto tiempo tarda en duplicarse un capital de 10000 euros al n por ciento anual, siendo n un nº leído desde teclado. Obtener el mismo valor, pero el pago de intereses se hace mensualmente.
Solución Ejercicio 27.
Planteamiento del problema
La fórmula del interés compuesto es la siguiente:
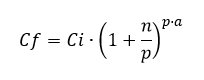
Donde:
Cf – es el capital final que se obtiene.
Ci – es el capital inicial.
n – es la tasa de interés anual en decimal (por ejemplo, 2% sería 0,02)
p – es el número de pagos de intereses en el año (para pago anual, 1, para pago mensual 12)
a – es el número de años.
El programa va calculando Cf para 1 año, 2 años, 3 años, etc, hasta que se consigue un Cf mayor o igual a 20000, el doble de lo invertido.
#include <stdio.h>
#include <math.h>
int main(void) {
float n,ci,cf; /* n %tasa anual, ci capital inicial, cf capital final */
int a; /* años transcurridos */
printf("Introduzca tasa de interés anual: ");
scanf("%f",&n);
ci = 10000; /* capital inicial */
printf("Pago de intereses anualmente:\n");
a=0;
while(cf<20000) {
a++;
cf = ci * pow((1+n/100.0),a);
}
printf("El capital es de %.2f al cabo de %d años.\n\n",cf,a);
printf("Pago de intereses mensualmente:\n");
a=0;
cf=0;
while(cf<20000) {
a++;
cf = ci * pow(1+((n/100.0)/12.0),12*a);
}
printf("El capital es de %.2f al cabo de %d años.\n\n",cf,a);
return 0;
}
Ejercicio 28.
Escribir un programa que lea un número escrito por el usuario que esté entre 1 y 10. El programa debe seguir pidiendo el número al usuario hasta que sea correcto.
Solución Ejercicio 28.
#include <stdio.h>
int main(void) {
int n;
printf("Introduzca un número entre 1 y 10: ");
scanf("%d",&n);
while(n<1 || n>10) {
printf("Error. El número debe estar entre 1 y 10.\n");
printf("Introduzca un número entre 1 y 10: ");
scanf("%d",&n);
}
printf("Ok. Gracias.\n");
return 0;
}
Ejercicio 29.
Escribir un programa que pida un número del 1 al 9, y escriba por pantalla la tabla de multiplicar correspondiente.
Solución Ejercicio 29.
#include <stdio.h>
int main(void) {
int i,n,m;
printf("Introduzca un número entre 1 y 9: ");
scanf("%d",&n);
if(n<1 || n>9) {
printf("Error. El número introducido debe estar entre 1 y 9.\n");
} else {
for(i=0;i<=10;i++) {
m = i * n;
printf("%d x %d = %d\n",n,i,m);
}
}
return 0;
}
Ejercicio 30.
Escribe un programa que pide dos números de 3 y 2 cifras respectivamente, e imprima por pantalla el resultado de la multiplicación de ambos números tal y como lo haríamos a mano. Sean M=739, y N=12.
7 3 9 x 1 2 ----- 1 4 7 8 7 3 9 ------- 8 8 6 8
Solución Ejercicio 30.
Planteamiento del problema
Será necesario calcular tres multiplicaciones:
Esta será la multiplicación final m: 739 x 12 = 8868
Esta otra será la multiplicación parcial m1: 739 x 2 = 1478
Y esta será la multiplicación parcial m2: 739 x 1 = 739
Para obtener el 2 (unidades de 12), bastará con calcular el resto de 12/10.
Para obtener el 1 (decenas de 12), bastará con calcular el cociente de 12/10. Una vez calculadas las multiplicaciones, solo hay que colocar cada número en la línea adecuada. Hay que controlar la cantidad de espacios que se imprimen delante de cada línea para que los números queden alineados. Esto dependerá de lo grande que sea el número a mostrar.
#include <stdio.h>
int main(void) {
int a,b;
/* a - número de 3 cifras, b - número de 2 cifras */
int m1,m2,m;
/* m1 y m2 - multiplicaciones intermedias, m - multiplicación final */
printf("Introduzca un número de tres cifras: ");
scanf("%d",&a);
printf("Introduzca un número de dos cifras: ");
scanf("%d",&b);
m = a * b; /* multiplicación final */
m1 = a * (b % 10); /* m1 es a por las unidades de b */
m2 = a * (b / 10); /* m2 es a por las decenas de b */
/*
Colocación de los números en forma de multiplicación.
Se añaden espacios al comienzo para que queden alineados.
*/
printf(" %d\n",a);
printf(" x%d\n",b);
printf(" ---\n");
if(m1>=1000) printf(" ");
else printf(" ");
printf("%d\n",m1);
if(m2<1000) printf(" ");
printf("%d\n",m2);
printf("-----\n");
if(m<10000) printf(" ");
printf("%d\n",m);
return 0;
}
Ejercicio 31.
Escriba un programa que dándole el importe exacto de una cantidad te indica el mínimo número de monedas y billetes que podrías tener. Las monedas son de 1 cent., 5 cent., 10 cent., 20 cent., 50 cent., 1 euro, 2 euros, 10 euros, 50 euros, 100 euros y 500 euros.
Solución Ejercicio 31.
Planteamiento del problema
Se pasará la cantidad introducida a céntimos, y con esta cantidad, basta con hacer divisiones entre los valores (en céntimos) de cada billete o moneda para saber la cantidad de éstos. Se calculará el resto para obtener la cantidad sobrante y se usará esta cantidad para convertirla en nuevos billetes o monedas.
Al imprimir el resultado se usan if que comprueben si hay billetes o monedas de un valor, y si es así, se imprime el desglose.
#include <stdio.h>
int main(void) {
float cantidad;
int canticent;
/* billetes y monedas */
int b500,b100,b50,b10,m2,m1,m50c,m20c,m10c,m5c,m1c;
printf("Introduzca una cantidad de euros: ");
scanf("%f",&cantidad);
canticent = (int) (cantidad * 100); /* paso a centimos */
b500 = canticent / 50000; /* billetes de 500 */
canticent = canticent % 50000; /* centimos sobrantes */
b100 = canticent / 10000; /* billetes de 100 */
canticent = canticent % 10000; /* centimos sobrantes */
b50 = canticent / 5000; /* billetes de 50 */
canticent = canticent % 5000; /* centimos sobrantes */
b10 = canticent / 1000; /* billetes de 10 */
canticent = canticent % 1000; /* centimos sobrantes */
m2 = canticent / 200; /* monedas de 2 */
canticent = canticent % 200; /* centimos sobrantes */
m1 = canticent / 100; /* monedas de 1 */
canticent = canticent % 100; /* centimos sobrantes */
m50c = canticent / 50; /* monedas de 50 cent */
canticent = canticent % 50; /* centimos sobrantes */
m20c = canticent / 20; /* monedas de 20 cent */
canticent = canticent % 20; /* centimos sobrantes */
m10c = canticent / 10; /* monedas de 10 cent */
canticent = canticent % 10; /* centimos sobrantes */
m5c = canticent / 5; /* monedas de 5 cent */
canticent = canticent % 5; /* centimos sobrantes */
m1c = canticent % 5; /* monedas de 1 cent */
printf("%.2f son: \n",cantidad);
if(b500>0) printf("%d billetes de 500\n",b500);
if(b100>0) printf("%d billetes de 100\n",b100);
if(b50>0) printf("%d billetes de 50\n",b50);
if(b10>0) printf("%d billetes de 10\n",b10);
if(m2>0) printf("%d monedas de 2\n",m2);
if(m1>0) printf("%d monedas de 1\n",m1);
if(m50c>0) printf("%d monedas de 50 cent.\n",m50c);
if(m20c>0) printf("%d monedas de 20 cent.\n",m20c);
if(m10c>0) printf("%d monedas de 10 cent.\n",m10c);
if(m5c>0) printf("%d monedas de 5 cent.\n",m5c);
if(m1c>0) printf("%d monedas de 1 cent.\n",m1c);
return 0;
}
Ejercicio 32.
Un número binario representa valores mediante combinaciones de ceros y unos. Un número binario de cuatro dígitos puede ser convertido a su correspondiente valor decimal como en el ejemplo:
11002 = 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 = 1210
Realizar un programa que admita números en base 2 de 8 cifras, y los convierta al correspondiente valor decimal.
Solución Ejercicio 12.
Planteamiento del problema
En la solución se usa un bucle que se repite 8 veces y que va tomando cada bit desde la derecha. Según el bit, se calcula la potencia de 2 correspondiente y se suma a la variable dec, que finalmente tendrá el valor en decimal.
#include <stdio.h>
#include <math.h>
int main(void) {
int bit,bin,dec,baux; /* baux - variable auxiliar */
int i;
printf("Introduzca un número binario de 8 cifras: ");
scanf("%d",&bin);
baux = bin;
dec = 0;
for(i=0;i<8;i++) { /* i va tomando los exponentes de 2 para cada bit */
bit = baux % 10;
/* tomo el bit más a la derecha */
if(bit==1)
dec = dec + pow(2,i);
/* solo si el bit es 1 calculo la potencia de 2 correspondiente */
baux = baux / 10;
/* y elimino el 0 o 1 más a la derecha para comprobar el siguiente bit */
}
printf("%d en binario es igual a %d en decimal.\n",bin,dec);
return 0;
}
Ejercicio 33.
Un tren expreso parte del punto A al punto B a velocidad constante (V1), y a la vez un tren rápido sale del punto B hacia el punto A a velocidad constante (V2). Inicialmente, la «hormiga atómica» se encuentra posada en el tren expreso, y parte hacia el tren rápido a velocidad constante (V3), para darle encuentro. Cuando llega a él, y sin descansar, vuela de vuelta al tren expreso. Da la vuelta, vuelve al tren rápido. Da la vuelta y vuelve al tren expreso, etc. Realizar un programa tal que, dada la distancia entre A y B, la velocidad del tren expreso V1, la velocidad del tren rápido V2 y la velocidad de la «hormiga atómica» V3, calcule qué distancia ha recorrido la «hormiga atómica» hasta que es triturada por encontrarse entre ambos trenes cuando estos chocan entre sí. Para resolver el problema suponer que la línea entre A y B es recta y que se cumple que
0 < V1 < V2 < V1 + V2 < V3
Nota: tratar de encontrar la solución elegante del problema, y programar la solución mediante la «fuerza bruta».
Solución Ejercicio 33.
Planteamiento del problema
Al cabo de un tiempo t, la hormiga atómica ha recorrido una distancia d3 a una velocidad V3, el tren expreso (1) ha recorrido una distancia d1 a una velocidad V1, y el tren rápido (2) ha recorrido una distancia d2 a una velocidad V2:

Las velocidades son las siguientes:
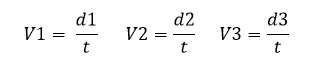
Despejando t e igualándolo para las velocidades V2 y V3 tenemos:
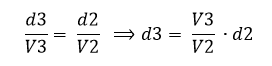
Como d2 = d – d3, tenemos:
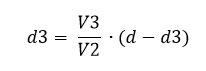
Y operando y despejando d3 se obtiene:
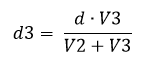
Esta es la distancia recorrida por la hormiga atómica en el primer viaje. Esta distancia habría que sumarla a un acumulador total que nos dará la distancia total recorrida por la hormiga.
En esta situación, la hormiga está en el tren rápido, y se podría considerar que la situación es la inicial, solo que ahora tendremos una nueva d’.

La nueva d’ será: d’ = d3 – d1
Sabiendo las velocidades V1 y V3 tenemos:
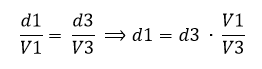
Sustituyendo en la igualdad anterior tenemos:
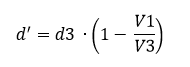
Una vez calculada la nueva d, se repite el proceso calculando la nueva distancia d3’ recorrida por la hormiga atómica, en este caso en dirección contraria, que sería:
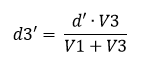
Y se calcula la nueva d’’, que ahora sería:
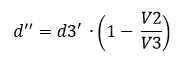
Este proceso se repite, sumando cada d3 calculado en el total, hasta que la d sea 0 (hay colisión entre los trenes)
Para controlar la dirección que toma la hormiga, se usa una variable direccion que toma los valores 1 y -1 consecutivamente, según si la hormiga vuela hacia la derecha o izquierda.
#include <stdio.h>
int main(void) {
float v1,v2,v3,d,d3,total=0;
int direccion = 1; /* es 1 si la hormiga va a la derecha
es -1 si la hormiga va a la izquierda
*/
printf("Introduzca la distancia inicial d: ");
scanf("%f",&d);
printf("Introduzca la velocidad v1 (tren expreso): ");
scanf("%f",&v1);
printf("Introduzca la velocidad v2 (tren rápido): ");
scanf("%f",&v2);
printf("Introduzca la velocidad v3 (hormiga atómica): ");
scanf("%f",&v3);
if(v1>0 && v1<v2 && v2 < (v1+v2) && (v1+v2) < v3) {
/* las velocidades introducidas son correctas */
while(d>0) {
if(direccion==1)
d3 = (d * v3) / (v2 + v3);
else if(direccion==-1)
d3 = (d * v3) / (v1 + v3);
total += d3;
if(direccion==1)
d = d3 * (1 - (v1/v3));
else
d = d3 * (1 - (v2/v3));
direccion = direccion * (-1); /* cambio de direccion */
}
printf("La distancia recorrida por la hormiga atomica es:
%.2f\n",total);
} else {
printf("Las velocidades no son correctas.\n");
printf("Debe cumplirse: 0 < v1 < v2 < v1+v2 < v3\n");
}
return 0;
}
Ejercicio 34.
Dada una serie de n puntos (xi, yi, i=1,2,…n), encontrar los coeficientes de la recta dada por la ecuación y = mx + b que mejor ajusta a dichos puntos. Para ello, realizar el siguiente cálculo:
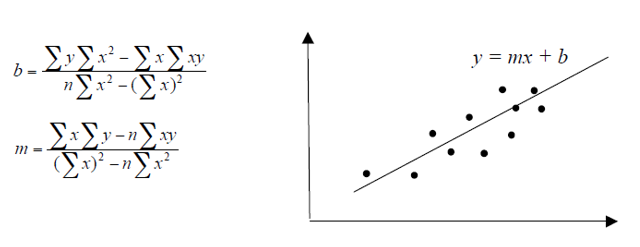
Hacer el programa para que vaya calculando las sumas conforme se van leyendo valores de x e y, y mostrar el resultado cuando x=0, y=0.
Ej: si x={1,2,3,4,5} e y={1,2,2,4,4}, los parámetros de la recta óptima son m=0.8, b=0.2
Solución Ejercicio 34.
Planteamiento del problema
Se usa un contador n para contar el número de puntos introducidos.
Por otro lado, se usan varias variables acumuladoras para mantener cada sumatorio. Luego simplemente se usan esos sumatorios y n para calcular los valores actualizados de m y b.
#include <stdio.h>
#include <math.h>
int main(void) {
float x,y;
/* suma de y, suma de x^2, suma de x, suma de x*y */
float sy=0,sx2=0,sx=0,sxy=0;
int n=0; /* número de puntos introducidos */
float m,b; /* m y b calculados */
printf("Introduzca x,y:");
scanf("%f,%f",&x,&y);
while(!(x==0 && y==0)) {
n++; /* hay un punto más */
/* sumatorios... */
sy += y;
sx2 += (x*x);
sx += x;
sxy += (x*y);
b = ((sy*sx2)-(sx*sxy)) / ((n*sx2) - pow(sx,2));
m = ((sx*sy)-(n*sxy)) / ( pow(sx,2) - (n*sx2));
printf("Introduzca x,y:");
scanf("%f,%f",&x,&y);
}
printf("m = %.2f b = %.2f\n",m,b);
return 0;
}
Ejercicio 35.
Un número decimal se puede convertir al correspondiente valor binario realizando sucesivas divisiones por 2, y tomando el valor del resto como cifra binaria. Realizar un programa que admita números en base decimal entre 0 y 32000, y los convierta al correspondiente valor binario.
Solución Ejercicio 35.
Planteamiento del problema
El programa va dividiendo el número decimal y cada resto que obtiene lo multiplica por una potencia de 10, para así obtener en decimal una representación del número binario resultante. (Ejemplo: el 3 en binario sería 11, es decir once representado en decimal)
El problema es que el número 32000 pasado a binario sería el: 111110100000000 (111 billones … etc). Para almacenar este valor en una variable como un valor decimal, es necesario variables double, que son capaces de guardar valores grandes.
int main(void) {
int dec,decaux; /*decaux, decimal auxiliar */
double bin;
int exp,bit;
printf("Introduzca un número decimal entre 0 y 32000: ");
scanf("%d",&dec);
decaux = dec;
bin = 0;
exp = 0; /* exponentes para las potencias de 10 */
while(decaux>1) { /* mientras se pueda dividir entre 2 */
bit = decaux % 2; /* obtiene el bit correspondiente */
bin = bin + bit*pow(10,exp);
/* lo representa en decimal, en una variable double, a través
de sumas de potencias de 10 */
decaux = decaux / 2; /* y sigo el proceso con el cociente obtenido */
exp++; /* incremento el exponente */
}
/* el último cociente también forma parte del número binario */
bin = bin + decaux*pow(10,exp);
printf("%d en decimal es igual a %.0f en binario.\n",dec,bin);
return 0;
}
Ejercicio 36.
Realizar un programa para realizar cambios de base. Es decir, tomando como dato la expresión de un número, la base en la que está expresado dicho número, y la base de destino, el programa será capaz de escribir la representación de un número en cualquier base. (Considerar todas aquellas bases entre 2 y 16 inclusive)
Solución Ejercicio 36.
Planteamiento del problema
La solución general del problema es tomar el número con la base inicial b1 y convertirlo a decimal. A continuación, tomar el número decimal obtenido y convertirlo a la base b2.
Para introducir un número en hexadecimal, son necesarios caracteres no numéricos (de la ‘A’ a la ‘F’). Por tanto, será necesario usar una cadena de caracteres para introducir el número a convertir, y también será necesario una cadena de caracteres para mostrar el número convertido. Por eso n1 y n2 en el programa son cadenas de caracteres.
Los caracteres ‘0’ al ‘9’ tienen un valor ASCII que va desde el 48 al 57. Por tanto, para convertir el carácter ‘0’ a 0, es necesario restarle a su valor ASCII el número 48. Igual con los demás caracteres numéricos.
Los caracteres ‘A’ a ‘F’ tienen valores ASCII desde el 65 al 70. Por tanto, para obtener los valores hexadecimales desde el 10 (A) al 15 (F) es necesario restar al carácter el valor 65 y sumarle 10.
Los caracteres ‘a’ a ‘f’ tienen valores ASCII desde el 97 al 102. Por tanto, para obtener los valores hexadecimales desde el 10 (a) al 15 (f) es necesario restar al carácter el valor 97 y sumarle 10.
En la conversión del número desde la base b1 a decimal, es necesario recorrer el número de derecha a izquierda, por lo que se usa una variable tam (tamaño) donde se guarda el tamaño del número y que sirve para comenzar a recorrerlo desde el final hasta el principio. Se usa la función strlen de la librería string.h para calcular el tamaño de la cadena.
En la conversión a la segunda base, los distintos restos obtenidos son almacenados en la cadena n2, al igual que el último cociente. El problema es que de esta forma el número queda almacenado al revés. Por eso es necesario usar la función strrev de la librería string.h para darle la vuelta a la cadena.
#include <stdio.h>
#include <math.h>
#include <string.h>
int main(void) {
char n1[50];
char n2[50];
int aux,tam,i,exp,digit;
int b1, b2;
printf("Introduzca numero: ");
scanf("%s",n1);
printf("Indique la base en la que está: ");
scanf("%d",&b1);
printf("Indique la base a la que lo quiere convertir: ");
scanf("%d",&b2);
if(b1>=2 && b1<=16 && b2>=2 && b2<=16) {
/* conversión a decimal */
tam = strlen(n1); /* nº de digitos del numero */
exp = 0; /* exponentes */
aux = 0; /* valor del número en decimal */
/* recorre la cadena de derecha a izquierda */
for(i=tam-1;i>=0;i--) {
/* si hay un dígito entre 0 y 9 lo convierte a su valor */
if(n1[i]>='0' && n1[i]<='9') {
digit = n1[i]-48;
/* si es un dígito-letra entre A y F lo convierte a su valor */
} else if(n1[i]>='A' && n1[i]<='F') {
digit = n1[i]-65+10;
} else if(n1[i]>='a' && n1[i]<='f') {
digit = n1[i]-97+10;
}
/* calcula la suma de productos de potencias de la base */
aux = aux + digit * pow(b1,exp);
exp++;
}
printf("El numero en decimal es %d\n",aux);
/* conversión a la base destino */
/* se hace por divisiones sucesivas */
tam=0;
while(aux>=b2) { /* mientras se puede dividir entre la base */
digit = aux % b2; /* el dígito es el resto de la división */
/* si el dígito está entre 0 y 9 se almacena el caracter
entre '0' y '9' */
if(digit>=0 && digit<=9) {
n2[tam]=digit+48;
/* si el dígito tiene un valor superior a 10, se convierte al
caracter entre 'A' y 'F' */
} else if(digit>=10 && digit<=15) {
n2[tam]=digit+65-10;
}
tam++;
/* y se obtiene el cociente de la división para
repetir el proceso */
aux = aux/b2;
}
/* el último cociente también forma parte del número convertido: */
if(aux>=0 && aux<=9) {
n2[tam]=aux+48;
} else if(aux>=10 && aux<=15) {
n2[tam]=aux+65-10;
}
tam++;
n2[tam]='\0'; /* para que la cadena del numero 2 sea correcta, debe
terminar en '\0' */
strrev(n2); /* el número obtenido está al revés, por lo que se le da
la vuelta */
printf("El número en base %d es %s\n",b2,n2);
} else {
printf("Las bases deben estar entre 2 y 16.\n");
}
return 0;
}
Ejercicio 37.
Escribir un programa que calcule la suma de los n primeros términos de la serie:
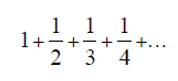
Solución Ejercicio 37.
#include <stdio.h>
int main(void) {
int n,i;
float suma = 0;
printf("Intoduzca n: ");
scanf("%d",&n);
for(i=1;i<=n;i++) {
/* convierto i a float para asegurar una división real */
suma = suma + (1.0/(float)i);
}
printf("La suma es: %.2f\n",suma);
return 0;
}
Ejercicio 38.
Escribir un programa que sume la serie:
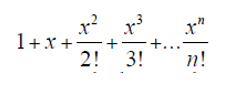
hacia adelante y hacia atrás, comparando los resultados. ¿Es fiable esta suma para calcular el valor de e^x, para todos los valores de x?
Solución Ejercicio 38.
Notas:
La serie sumará lo mismo independientemente de que se sume desde 1 a xn/n! o desde xn/n! a 1.
Para que la suma sea fiable para calcular el valor de ex es necesario que n sea grande. De hecho, cuanto más grande sea x, más grande tendrá que ser n para que el resultado sea cercano a ex. Para comprobar esto, el programa le pide al usuario un valor n, y calcula con ese valor la suma de la serie para los valores de x = 1 hasta 10, comparando los resultados con el valor correspondiente de ex y calculando el error producido.
Se puede observar que para n pequeñas, la suma de la serie para x grandes da grandes errores.
Ejemplo 1. Se introduce n=20, y se comprueba que los errores son pequeños:
Introduzca n: 20
x=1.00 La suma es 2.72 e elevado a 1 es 2.72 Error: 0.00
x=2.00 La suma es 7.39 e elevado a 2 es 7.39 Error: 0.00
x=3.00 La suma es 20.09 e elevado a 3 es 20.09 Error: 0.00
x=4.00 La suma es 54.60 e elevado a 4 es 54.60 Error: 0.00
x=5.00 La suma es 148.41 e elevado a 5 es 148.41 Error: 0.00
x=6.00 La suma es 403.43 e elevado a 6 es 403.43 Error: 0.00
x=7.00 La suma es 1096.62 e elevado a 7 es 1096.63 Error: 0.02
x=8.00 La suma es 2980.68 e elevado a 8 es 2980.96 Error: 0.28
x=9.00 La suma es 8099.52 e elevado a 9 es 8103.08 Error: 3.56
x=10.00 La suma es 21991.48 e elevado a 10 es 22026.46 Error: 34.98
Ejemplo 2. Se introduce n=5, y se comprueba que los errores son mayores a partir de valores pequeños de x.
Introduzca n: 5
x=1.00 La suma es 2.72 e elevado a 1 es 2.72 Error: 0.00
x=2.00 La suma es 7.27 e elevado a 2 es 7.39 Error: 0.12
x=3.00 La suma es 18.40 e elevado a 3 es 20.09 Error: 1.69
x=4.00 La suma es 42.87 e elevado a 4 es 54.60 Error: 11.73
x=5.00 La suma es 91.42 e elevado a 5 es 148.41 Error: 57.00
x=6.00 La suma es 179.80 e elevado a 6 es 403.43 Error: 223.63
x=7.00 La suma es 329.77 e elevado a 7 es 1096.63 Error: 766.87
x=8.00 La suma es 570.07 e elevado a 8 es 2980.96 Error: 2410.89
x=9.00 La suma es 937.45 e elevado a 9 es 8103.08 Error: 7165.63
x=10.00 La suma es 1477.67 e elevado a 10 es 22026.46 Error: 20548.80
#include <stdio.h>
#include <math.h>
int main(void) {
float x,pe,error;
int n,i,j;
float f,pot;
float suma;
//printf("Introduzca x: ");
//scanf("%f",&x);
printf("Introduzca n: ");
scanf("%d",&n);
for(x=1;x<=10;x++) {
suma=0;
for(i=0;i<=n;i++) {
pot = pow(x,i);
f=1;
for(j=1;j<=i;j++) {
f = f * j;
}
suma += pot/f;
}
printf("\nx=%.2f La suma es %.2f ",x,suma);
pe = exp(x);
printf("e elevado a %.0f es %.2f ",x,pe);
error = suma-pe;
error = (error<0)?-error:error;
printf("Error: %.2f\n",error);
}
return 0;
}
Ejercicio 39.
Un número «perfecto» es un entero positivo tal que es igual a la suma de sus factores. Por ejemplo, el número 28 es igual a la suma de 1 + 2 + 4 + 7 + 14. Realizar un programa que calcule los números perfectos entre 1 y 30.000.
Solución Ejercicio 39.
#include <stdio.h>
int main(void) {
int n=28,f,suma;
for(n=1;n<30000;n++) {
suma=0;
/* Los factores a buscar están comprendidos
* entre 1 y la mitad del número.
*/
for(f=1;f<=(n/2);f++) {
if(n%f==0)
suma+=f;
}
if(suma==n)
printf("El %d es un número perfecto.\n",n);
}
return 0;
}
Ejercicio 40.
Determinar los términos de la sucesión
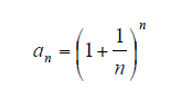
para n=1, 2, 3, etc. ¿ A qué número converge ?
Solución Ejercicio 40.
Nota:
Se generan 10000 términos de la sucesión para comprobar hacia donde converge, y se ve que la sucesión converge hacia el número e.
#include <stdio.h>
#include <math.h>
int main(void) {
float a;
int n;
for(n=1;n<=10000;n++) {
a = pow(1.0 + (1.0/(float)n), n);
printf("%.4f ",a);
}
return 0;
}
Puedes acceder a más recursos formativos, ejercicios resueltos de programación, test de informática, etc., en ejerciciosmesa.com. También tienes disponibles juegos de lógica e interactivos en mesagames.es.
